Find All Solutions to System of Linear Equations

1 System of Linear Equations

Practical problems in many fields of study—such as biology, business, chemistry, computer science, economics, electronics, engineering, physics and the social sciences—can often be reduced to solving a system of linear equations. Linear algebra arose from attempts to find systematic methods for solving these systems, so it is natural to begin this book by studying linear equations.

If , , and are real numbers, the graph of an equation of the form

$\begin{equation*} ax + by = c \end{equation*}$

is a straight line (if and are not both zero), so such an equation is called a linear equation in the variables and . However, it is often convenient to write the variables as $x_1, x_2, \dots, x_n$ , particularly when more than two variables are involved. An equation of the form

$\begin{equation*} a_1x_1 + a_2x_2 + \dots + a_nx_n = b \end{equation*}$

is called a linear equation in the variables $x_1, x_2, \dots, x_n$ . Here $a_1, a_2, \dots, a_n$ denote real numbers (called the coefficients of $x_1, x_2, \dots, x_n$ , respectively) and is also a number (called the constant term of the equation). A finite collection of linear equations in the variables $x_1, x_2, \dots, x_n$ is called a system of linear equationsin these variables. Hence,

$\begin{equation*} 2x_1 - 3x_2 + 5x_3 = 7 \end{equation*}$

is a linear equation; the coefficients of , , and are , , and , and the constant term is . Note that each variable in a linear equation occurs to the first power only.

Given a linear equation $a_1x_1 + a_2x_2 + \dots + a_nx_n = b$ , a sequence $s_1, s_2, \dots, s_n$ of numbers is called a solution to the equation if

$\begin{equation*} a_1s_1 + a_2s_2 + \dots + a_ns_n = b \end{equation*}$

that is, if the equation is satisfied when the substitutions $x_1 = s_1, x_2 = s_2, \dots, x_n = s_n$ are made. A sequence of numbers is called a solution to a systemof equations if it is a solution to every equation in the system.

A system may have no solution at all, or it may have a unique solution, or it may have an infinite family of solutions. For instance, the system , has no solution because the sum of two numbers cannot be 2 and 3 simultaneously. A system that has no solution is called inconsistent; a system with at least one solution is called consistent.

Show that, for arbitrary values of and ,

$\begin{align*} x_1 &= t - s + 1 \\ x_2 &= t + s + 2 \\ x_3 &= s\\ x_4 &= t \end{align*}$

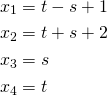
is a solution to the system

$\begin{equation*} \arraycolsep=1pt \begin{array}{rrrrrrr} x_1 & - & 2x_2 & + 3x_3 & + x_4 & = & -3\\ 2x_1 & -& x_2 & + 3x_3 & - x_4 & = & 0 \end{array} \end{equation*}$

Simply substitute these values of , , , and in each equation.

$\begin{align*} x_1 - 2x_2 + 3x_3 + x_4 &= (t - s + 1) - 2(t + s + 2) + 3s + t = -3\\ 2x_1 - x_2 + 3x_3 - x_4 &= 2(t - s + 1) - (t + s + 2) + 3s - t = 0 \end{align*}$

Because both equations are satisfied, it is a solution for all choices of and .

The quantities and in this example are called parameters, and the set of solutions, described in this way, is said to be given in parametric formand is called the general solutionto the system. It turns out that the solutions to every system of equations (if there are solutions) can be given in parametric form (that is, the variables , , $\dots$ are given in terms of new independent variables , , etc.).

When only two variables are involved, the solutions to systems of linear equations can be described geometrically because the graph of a linear equation is a straight line if and are not both zero. Moreover, a point with coordinates and lies on the line if and only if —that is when , is a solution to the equation. Hence the solutions to a system of linear equations correspond to the points that lie on all the lines in question.

In particular, if the system consists of just one equation, there must be infinitely many solutions because there are infinitely many points on a line. If the system has two equations, there are three possibilities for the corresponding straight lines:

The lines intersect at a single point. Then the system has a unique solution corresponding to that point.
The lines are parallel (and distinct) and so do not intersect. Then the system has no solution.
The lines are identical. Then the system has infinitely many solutions—one for each point on the (common) line.

With three variables, the graph of an equation can be shown to be a plane and so again provides a "picture" of the set of solutions. However, this graphical method has its limitations: When more than three variables are involved, no physical image of the graphs (called hyperplanes) is possible. It is necessary to turn to a more "algebraic" method of solution.

Before describing the method, we introduce a concept that simplifies the computations involved. Consider the following system

$\begin{equation*} \arraycolsep=1pt \begin{array}{rlrlrlrcr} 3x_1 & + & 2x_2 & - & x_3 & + & x_4 & = & -1\\ 2x_1 & & & - & x_3 & + & 2x_4 & = & 0\\ 3x_1 & + & x_2 & + & 2x_3 & + & 5x_4 & = & 2 \end{array} \end{equation*}$

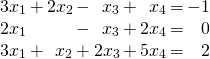
of three equations in four variables. The array of numbers

$\begin{equation*} \left[ \begin{array}{rrrr|r} 3 & 2 & -1 & 1 & -1 \\ 2 & 0 & -1 & 2 & 0 \\ 3 & 1 & 2 & 5 & 2 \end{array} \right] \end{equation*}$

occurring in the system is called the augmented matrixof the system. Each row of the matrix consists of the coefficients of the variables (in order) from the corresponding equation, together with the constant term. For clarity, the constants are separated by a vertical line. The augmented matrix is just a different way of describing the system of equations. The array of coefficients of the variables

$\begin{equation*} \left[ \begin{array}{rrrr} 3 & 2 & -1 & 1 \\ 2 & 0 & -1 & 2 \\ 3 & 1 & 2 & 5 \end{array} \right] \end{equation*}$

is called the coefficient matrixof the system and
$\left[ \begin{array}{r} -1 \\ 0 \\ 2 \end{array} \right]$ is called the constant matrixof the system.

Elementary Operations

The algebraic method for solving systems of linear equations is described as follows. Two such systems are said to be equivalent if they have the same set of solutions. A system is solved by writing a series of systems, one after the other, each equivalent to the previous system. Each of these systems has the same set of solutions as the original one; the aim is to end up with a system that is easy to solve. Each system in the series is obtained from the preceding system by a simple manipulation chosen so that it does not change the set of solutions.

As an illustration, we solve the system , in this manner. At each stage, the corresponding augmented matrix is displayed. The original system is

$\begin{equation*} \begin{array}{lcl} \arraycolsep=1pt \begin{array}{rlrcr} x & + & 2y & = & -2 \\ 2x & + & y & = & 7 \end{array} & \quad & \left[ \begin{array}{rr|r} 1 & 2 & -2 \\ 2 & 1 & 7 \end{array} \right] \end{array} \end{equation*}$

First, subtract twice the first equation from the second. The resulting system is

$\begin{equation*} \begin{array}{lcl} \arraycolsep=1pt \begin{array}{rlrcr} x & + & 2y & = & -2 \\ & - & 3y & = & 11 \end{array} & \quad & \left[ \begin{array}{rr|r} 1 & 2 & -2 \\ 0 & -3 & 11 \end{array} \right] \end{array} \end{equation*}$

which is equivalent to the original. At this stage we obtain $y = -\frac{11}{3}$ by multiplying the second equation by $-\frac{1}{3}$ . The result is the equivalent system

$\begin{equation*} \begin{array}{lcl} \arraycolsep=1pt \begin{array}{rcr} x + 2y & = & -2 \\ y & = & -\frac{11}{3} \end{array} & \quad & \left[ \begin{array}{rr|r} 1 & 2 & -2 \\ 0 & 1 & -\frac{11}{3} \end{array} \right] \end{array} \end{equation*}$

Finally, we subtract twice the second equation from the first to get another equivalent system.

$\begin{equation*} \begin{array}{lcl} \def\arraystretch{1.5} \arraycolsep=1pt \begin{array}{rcr} x & = & \frac{16}{3} \\ y & = & -\frac{11}{3} \end{array} & \quad \quad & \def\arraystretch{1.5} \left[ \begin{array}{rr|r} 1 & 0 & \frac{16}{3} \\ 0 & 1 & -\frac{11}{3} \end{array} \right] \end{array} \end{equation*}$

Now this system is easy to solve! And because it is equivalent to the original system, it provides the solution to that system.

Observe that, at each stage, a certain operation is performed on the system (and thus on the augmented matrix) to produce an equivalent system.

The following operations, called elementary operations, can routinely be performed on systems of linear equations to produce equivalent systems.

Interchange two equations.
Multiply one equation by a nonzero number.
Add a multiple of one equation to a different equation.

Suppose that a sequence of elementary operations is performed on a system of linear equations. Then the resulting system has the same set of solutions as the original, so the two systems are equivalent.

Elementary operations performed on a system of equations produce corresponding manipulations of the rows of the augmented matrix. Thus, multiplying a row of a matrix by a number means multiplying every entry of the row by . Adding one row to another row means adding each entry of that row to the corresponding entry of the other row. Subtracting two rows is done similarly. Note that we regard two rows as equal when corresponding entries are the same.

In hand calculations (and in computer programs) we manipulate the rows of the augmented matrix rather than the equations. For this reason we restate these elementary operations for matrices.

The following are called elementary row operations on a matrix.

Interchange two rows.
Multiply one row by a nonzero number.
Add a multiple of one row to a different row.

In the illustration above, a series of such operations led to a matrix of the form

$\begin{equation*} \left[ \begin{array}{rr|r} 1 & 0 & * \\ 0 & 1 & * \end{array} \right] \end{equation*}$

where the asterisks represent arbitrary numbers. In the case of three equations in three variables, the goal is to produce a matrix of the form

$\begin{equation*} \left[ \begin{array}{rrr|r} 1 & 0 & 0 & * \\ 0 & 1 & 0 & * \\ 0 & 0 & 1 & * \end{array} \right] \end{equation*}$

This does not always happen, as we will see in the next section. Here is an example in which it does happen.

$\begin{equation*} \arraycolsep=1pt \begin{array}{rlrlrcr} 3x & + & 4y & + & z & = & 1 \\ 2x & + & 3y & & & = & 0 \\ 4x & + & 3y & - & z & = & -2 \end{array} \end{equation*}$

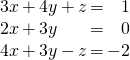
Solution:
The augmented matrix of the original system is

$\begin{equation*} \left[ \begin{array}{rrr|r} 3 & 4 & 1 & 1 \\ 2 & 3 & 0 & 0 \\ 4 & 3 & -1 & -2 \end{array} \right] \end{equation*}$

To create a in the upper left corner we could multiply row 1 through by $\frac{1}{3}$ . However, the can be obtained without introducing fractions by subtracting row 2 from row 1. The result is

$\begin{equation*} \left[ \begin{array}{rrr|r} 1 & 1 & 1 & 1 \\ 2 & 3 & 0 & 0 \\ 4 & 3 & -1 & -2 \end{array} \right] \end{equation*}$

The upper left is now used to "clean up" the first column, that is create zeros in the other positions in that column. First subtract times row 1 from row 2 to obtain

$\begin{equation*} \left[ \begin{array}{rrr|r} 1 & 1 & 1 & 1 \\ 0 & 1 & -2 & -2 \\ 4 & 3 & -1 & -2 \end{array} \right] \end{equation*}$

Next subtract times row 1 from row 3. The result is

$\begin{equation*} \left[ \begin{array}{rrr|r} 1 & 1 & 1 & 1 \\ 0 & 1 & -2 & -2 \\ 0 & -1 & -5 & -6 \end{array} \right] \end{equation*}$

This completes the work on column 1. We now use the in the second position of the second row to clean up the second column by subtracting row 2 from row 1 and then adding row 2 to row 3. For convenience, both row operations are done in one step. The result is

$\begin{equation*} \left[ \begin{array}{rrr|r} 1 & 0 & 3 & 3 \\ 0 & 1 & -2 & -2 \\ 0 & 0 & -7 & -8 \end{array} \right] \end{equation*}$

Note that the last two manipulations did not affect the first column (the second row has a zero there), so our previous effort there has not been undermined. Finally we clean up the third column. Begin by multiplying row 3 by $-\frac{1}{7}$ to obtain

$\begin{equation*} \left[ \begin{array}{rrr|r} 1 & 0 & 3 & 3 \\ 0 & 1 & -2 & -2 \\ 0 & 0 & 1 & \frac{8}{7} \end{array} \right] \end{equation*}$

Now subtract times row 3 from row 1, and then add times row 3 to row 2 to get

$\begin{equation*} \def\arraystretch{1.5} \left[ \begin{array}{rrr|r} 1 & 0 & 0 & - \frac{3}{7} \\ 0 & 1 & 0 & \frac{2}{7} \\ 0 & 0 & 1 & \frac{8}{7} \end{array} \right] \end{equation*}$

The corresponding equations are $x = -\frac{3}{7}$ , $y = \frac{2}{7}$ , and $z = \frac{8}{7}$ , which give the (unique) solution.

The algebraic method introduced in the preceding section can be summarized as follows: Given a system of linear equations, use a sequence of elementary row operations to carry the augmented matrix to a "nice" matrix (meaning that the corresponding equations are easy to solve). In Example 1.1.3, this nice matrix took the form

$\begin{equation*} \left[ \begin{array}{rrr|r} 1 & 0 & 0 & * \\ 0 & 1 & 0 & * \\ 0 & 0 & 1 & * \end{array} \right] \end{equation*}$

The following definitions identify the nice matrices that arise in this process.

A matrix is said to be in row-echelon form (and will be called a row-echelon matrix if it satisfies the following three conditions:

All zero rows (consisting entirely of zeros) are at the bottom.
The first nonzero entry from the left in each nonzero row is a 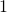, called the leading 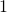for that row.
Each leading 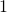is to the right of all leading 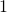s in the rows above it.

A row-echelon matrix is said to be in reduced row-echelon form (and will be called a reduced row-echelon matrixif, in addition, it satisfies the following condition:

4. Each leading is the only nonzero entry in its column.

The row-echelon matrices have a "staircase" form, as indicated by the following example (the asterisks indicate arbitrary numbers).

$\begin{equation*} \left[ \begin{array}{rrrrrrr} \multicolumn{1}{r|}{0} & 1 & * & * & * & * & * \\ \cline{2-3} 0 & 0 & \multicolumn{1}{r|}{0} & 1 & * & * & * \\ \cline{4-4} 0 & 0 & 0 & \multicolumn{1}{r|}{0} & 1 & * & * \\ \cline{5-6} 0 & 0 & 0 & 0 & 0 & \multicolumn{1}{r|}{0} & 1 \\ \cline{7-7} 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{array} \right] \end{equation*}$

The leading s proceed "down and to the right" through the matrix. Entries above and to the right of the leading s are arbitrary, but all entries below and to the left of them are zero. Hence, a matrix in row-echelon form is in reduced form if, in addition, the entries directly above each leading are all zero. Note that a matrix in row-echelon form can, with a few more row operations, be carried to reduced form (use row operations to create zeros above each leading one in succession, beginning from the right).

The importance of row-echelon matrices comes from the following theorem.

Every matrix can be brought to (reduced) row-echelon form by a sequence of elementary row operations.

In fact we can give a step-by-step procedure for actually finding a row-echelon matrix. Observe that while there are many sequences of row operations that will bring a matrix to row-echelon form, the one we use is systematic and is easy to program on a computer. Note that the algorithm deals with matrices in general, possibly with columns of zeros.

Step 1. If the matrix consists entirely of zeros, stop—it is already in row-echelon form.

Step 2. Otherwise, find the first column from the left containing a nonzero entry (call it ), and move the row containing that entry to the top position.

Step 3. Now multiply the new top row by to create a leading .

Step 4. By subtracting multiples of that row from rows below it, make each entry below the leading zero. This completes the first row, and all further row operations are carried out on the remaining rows.

Step 5. Repeat steps 1–4 on the matrix consisting of the remaining rows.

The process stops when either no rows remain at step 5 or the remaining rows consist entirely of zeros.

Observe that the gaussian algorithm is recursive: When the first leading has been obtained, the procedure is repeated on the remaining rows of the matrix. This makes the algorithm easy to use on a computer. Note that the solution to Example 1.1.3 did not use the gaussian algorithm as written because the first leading was not created by dividing row 1 by . The reason for this is that it avoids fractions. However, the general pattern is clear: Create the leading s from left to right, using each of them in turn to create zeros below it. Here is one example.

$\begin{equation*} \arraycolsep=1pt \begin{array}{rlrlrcr} 3x & + & y & - & 4z & = & -1 \\ x & & & + & 10z & = & 5 \\ 4x & + & y & + & 6z & = & 1 \end{array} \end{equation*}$

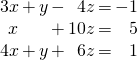
Solution:

The corresponding augmented matrix is

$\begin{equation*} \left[ \begin{array}{rrr|r} 3 & 1 & -4 & -1 \\ 1 & 0 & 10 & 5 \\ 4 & 1 & 6 & 1 \end{array} \right] \end{equation*}$

Create the first leading one by interchanging rows 1 and 2

$\begin{equation*} \left[ \begin{array}{rrr|r} 1 & 0 & 10 & 5 \\ 3 & 1 & -4 & -1 \\ 4 & 1 & 6 & 1 \end{array} \right] \end{equation*}$

Now subtract times row 1 from row 2, and subtract times row 1 from row 3. The result is

$\begin{equation*} \left[ \begin{array}{rrr|r} 1 & 0 & 10 & 5 \\ 0 & 1 & -34 & -16 \\ 0 & 1 & -34 & -19 \end{array} \right] \end{equation*}$

Now subtract row 2 from row 3 to obtain

$\begin{equation*} \left[ \begin{array}{rrr|r} 1 & 0 & 10 & 5 \\ 0 & 1 & -34 & -16 \\ 0 & 0 & 0 & -3 \end{array} \right] \end{equation*}$

This means that the following reduced system of equations

$\begin{equation*} \arraycolsep=1pt \begin{array}{rlrlrcr} x & & & + & 10z & = & 5 \\ & & y & - & 34z & = &-16 \\ & & & & 0 & = & -3 \end{array} \end{equation*}$

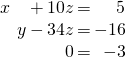
is equivalent to the original system. In other words, the two have the same solutions. But this last system clearly has no solution (the last equation requires that , and satisfy , and no such numbers exist). Hence the original system has no solution.

To solve a linear system, the augmented matrix is carried to reduced row-echelon form, and the variables corresponding to the leading ones are called leading variables. Because the matrix is in reduced form, each leading variable occurs in exactly one equation, so that equation can be solved to give a formula for the leading variable in terms of the nonleading variables. It is customary to call the nonleading variables "free" variables, and to label them by new variables $s, t, \dots$ , called parameters. Every choice of these parameters leads to a solution to the system, and every solution arises in this way. This procedure works in general, and has come to be called

To solve a system of linear equations proceed as follows:

Carry the augmented matrix\index{augmented matrix}\index{matrix!augmented matrix} to a reduced row-echelon matrix using elementary row operations.
If a row $\left[ \begin{array}{cccccc} 0 & 0 & 0 & \cdots & 0 & 1 \end{array} \right]$ occurs, the system is inconsistent.
Otherwise, assign the nonleading variables (if any) as parameters, and use the equations corresponding to the reduced row-echelon matrix to solve for the leading variables in terms of the parameters.

There is a variant of this procedure, wherein the augmented matrix is carried only to row-echelon form. The nonleading variables are assigned as parameters as before. Then the last equation (corresponding to the row-echelon form) is used to solve for the last leading variable in terms of the parameters. This last leading variable is then substituted into all the preceding equations. Then, the second last equation yields the second last leading variable, which is also substituted back. The process continues to give the general solution. This procedure is called back-substitution. This procedure can be shown to be numerically more efficient and so is important when solving very large systems.

Rank

It can be proven that the reduced row-echelon form of a matrix is uniquely determined by . That is, no matter which series of row operations is used to carry to a reduced row-echelon matrix, the result will always be the same matrix. By contrast, this is not true for row-echelon matrices: Different series of row operations can carry the same matrix to different row-echelon matrices. Indeed, the matrix $A = \left[ \begin{array}{rrr} 1 & -1 & 4 \\ 2 & -1 & 2 \end{array} \right]$ can be carried (by one row operation) to the row-echelon matrix $\left[ \begin{array}{rrr} 1 & -1 & 4 \\ 0 & 1 & -6 \end{array} \right]$ , and then by another row operation to the (reduced) row-echelon matrix $\left[ \begin{array}{rrr} 1 & 0 & -2 \\ 0 & 1 & -6 \end{array} \right]$ . However, it is true that the number of leading 1s must be the same in each of these row-echelon matrices (this will be proved later). Hence, the number depends only on and not on the way in which is carried to row-echelon form.

Compute the rank of $A = \left[ \begin{array}{rrrr} 1 & 1 & -1 & 4 \\ 2 & 1 & 3 & 0 \\ 0 & 1 & -5 & 8 \end{array} \right]$ .

Solution:

The reduction of to row-echelon form is

$\begin{equation*} A = \left[ \begin{array}{rrrr} 1 & 1 & -1 & 4 \\ 2 & 1 & 3 & 0 \\ 0 & 1 & -5 & 8 \end{array} \right] \rightarrow \left[ \begin{array}{rrrr} 1 & 1 & -1 & 4 \\ 0 & -1 & 5 & -8 \\ 0 & 1 & -5 & 8 \end{array} \right] \rightarrow \left[ \begin{array}{rrrr} 1 & 1 & -1 & 4 \\ 0 & 1 & -5 & 8 \\ 0 & 0 & 0 & 0 \end{array} \right] \end{equation*}$

Because this row-echelon matrix has two leading s, rank .

Suppose that rank , where is a matrix with rows and columns. Then $r \leq m$ because the leading s lie in different rows, and $r \leq n$ because the leading s lie in different columns. Moreover, the rank has a useful application to equations. Recall that a system of linear equations is called consistent if it has at least one solution.

Proof:

The fact that the rank of the augmented matrix is means there are exactly leading variables, and hence exactly nonleading variables. These nonleading variables are all assigned as parameters in the gaussian algorithm, so the set of solutions involves exactly parameters. Hence if , there is at least one parameter, and so infinitely many solutions. If , there are no parameters and so a unique solution.

Theorem 1.2.2 shows that, for any system of linear equations, exactly three possibilities exist:

No solution . This occurs when a row $\left[ \begin{array}{ccccc} 0 & 0 & \cdots & 0 & 1 \end{array} \right]$ occurs in the row-echelon form. This is the case where the system is inconsistent.
Unique solution . This occurs when every variable is a leading variable.
Infinitely many solutions . This occurs when the system is consistent and there is at least one nonleading variable, so at least one parameter is involved.

https://www.geogebra.org/m/cwQ9uYCZ
Please answer these questions after you open the webpage:
1. For the given linear system, what does each one of them represent?

2. Based on the graph, what can we say about the solutions? Does the system have one solution, no solution or infinitely many solutions? Why

3. Change the constant term in every equation to 0, what changed in the graph?

4. For the following linear system:

$\systeme*{x+y =0 ,y+z =0, x+z=0}$

Can you solve it using Gaussian elimination? When you look at the graph, what do you observe?

Many important problems involve linear inequalities rather than linear equations For example, a condition on the variables and might take the form of an inequality $2x - 5y \leq 4$ rather than an equality . There is a technique (called the simplex algorithm) for finding solutions to a system of such inequalities that maximizes a function of the form where and are fixed constants.

A system of equations in the variables $x_1, x_2, \dots, x_n$ is called homogeneous if all the constant terms are zero—that is, if each equation of the system has the form

$\begin{equation*} a_1x_1 + a_2x_2 + \dots + a_nx_n = 0 \end{equation*}$

Clearly $x_1 = 0, x_2 = 0, \dots, x_n = 0$ is a solution to such a system; it is called the trivial solution. Any solution in which at least one variable has a nonzero value is called a nontrivial solution.
Our chief goal in this section is to give a useful condition for a homogeneous system to have nontrivial solutions. The following example is instructive.

Show that the following homogeneous system has nontrivial solutions.

$\begin{equation*} \arraycolsep=1pt \begin{array}{rlrlrlrcr} x_1 & - & x_2 & + & 2x_3 & - & x_4 & = & 0 \\ 2x_1 & + &2x_2 & & & + & x_4 & = & 0 \\ 3x_1 & + & x_2 & + & 2x_3 & - & x_4 & = & 0 \end{array} \end{equation*}$

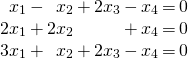
Solution:

The reduction of the augmented matrix to reduced row-echelon form is outlined below.

$\begin{equation*} \left[ \begin{array}{rrrr|r} 1 & -1 & 2 & -1 & 0 \\ 2 & 2 & 0 & 1 & 0 \\ 3 & 1 & 2 & -1 & 0 \end{array} \right] \rightarrow \left[ \begin{array}{rrrr|r} 1 & -1 & 2 & -1 & 0 \\ 0 & 4 & -4 & 3 & 0 \\ 0 & 4 & -4 & 2 & 0 \end{array} \right] \rightarrow \left[ \begin{array}{rrrr|r} 1 & 0 & 1 & 0 & 0 \\ 0 & 1 & -1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \end{array} \right] \end{equation*}$

The leading variables are , , and , so is assigned as a parameter—say . Then the general solution is , , , . Hence, taking (say), we get a nontrivial solution: , , , .

The existence of a nontrivial solution in Example 1.3.1 is ensured by the presence of a parameter in the solution. This is due to the fact that there is a nonleading variable ( in this case). But there must be a nonleading variable here because there are four variables and only three equations (and hence at most three leading variables). This discussion generalizes to a proof of the following fundamental theorem.

If a homogeneous system of linear equations has more variables than equations, then it has a nontrivial solution (in fact, infinitely many).

Proof:

Suppose there are equations in variables where , and let denote the reduced row-echelon form of the augmented matrix. If there are leading variables, there are nonleading variables, and so parameters. Hence, it suffices to show that . But $r \leq m$ because has leading 1s and rows, and by hypothesis. So $r \leq m < n$ , which gives .

Note that the converse of Theorem 1.3.1 is not true: if a homogeneous system has nontrivial solutions, it need not have more variables than equations (the system , has nontrivial solutions but .)

Theorem 1.3.1 is very useful in applications. The next example provides an illustration from geometry.

Solution:

Let the coordinates of the five points be , , , , and . The graph of passes through if

$\begin{equation*} ap_i^2 + bp_iq_i + cq_i^2 + dp_i + eq_i + f = 0 \end{equation*}$

This gives five equations, one for each , linear in the six variables , , , , , and . Hence, there is a nontrivial solution by Theorem 1.1.3. If , the five points all lie on the line with equation , contrary to assumption. Hence, one of , , is nonzero.

Linear Combinations and Basic Solutions

As for rows, two columns are regarded as equal if they have the same number of entries and corresponding entries are the same. Let $\vect{x}$ and $\vect{y}$ be columns with the same number of entries. As for elementary row operations, their sum $\vect{x} + \vect{y}$ is obtained by adding corresponding entries and, if is a number, the scalar product $k\vect{x}$ is defined by multiplying each entry of $\vect{x}$ by . More precisely:

$\begin{equation*} \mbox{If } \vect{x} = \left[ \begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right] \mbox{and } \vect{y} = \left[ \begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_n \end{array} \right] \mbox{then } \vect{x} + \vect{y} = \left[ \begin{array}{c} x_1 + y_1 \\ x_2 + y_2 \\ \vdots \\ x_n + y_n \end{array} \right] \mbox{and } k\vect{x} = \left[ \begin{array}{c} kx_1 \\ kx_2 \\ \vdots \\ kx_n \end{array} \right]. \end{equation*}$

A sum of scalar multiples of several columns is called a linear combination of these columns. For example, $s\vect{x} + t\vect{y}$ is a linear combination of $\vect{x}$ and $\vect{y}$ for any choice of numbers and .

Solution:

For $\vect{v}$ , we must determine whether numbers , , and exist such that $\vect{v} = r\vect{x} + s\vect{y} + t\vect{z}$ , that is, whether

$\begin{equation*} \left[ \begin{array}{r} 0 \\ -1 \\ 2 \end{array} \right] = r \left[ \begin{array}{r} 1 \\ 0 \\ 1 \end{array} \right] + s \left[ \begin{array}{r} 2 \\ 1 \\ 0 \end{array} \right] + t \left[ \begin{array}{r} 3 \\ 1 \\ 1 \end{array} \right] = \left[ \begin{array}{c} r + 2s + 3t \\ s + t \\ r + t \end{array} \right] \end{equation*}$

Equating corresponding entries gives a system of linear equations , , and for , , and . By gaussian elimination, the solution is , , and where is a parameter. Taking , we see that $\vect{v} = 2\vect{x} - \vect{y}$ is a linear combination of $\vect{x}$ , $\vect{y}$ , and $\vect{z}$ .

Turning to $\vect{w}$ , we again look for , , and such that $\vect{w} = r\vect{x} + s\vect{y} + t\vect{z}$ ; that is,

$\begin{equation*} \left[ \begin{array}{r} 1 \\ 1 \\ 1 \end{array} \right] = r \left[ \begin{array}{r} 1 \\ 0 \\ 1 \end{array} \right] + s \left[ \begin{array}{r} 2 \\ 1 \\ 0 \end{array} \right] + t \left[ \begin{array}{r} 3 \\ 1 \\ 1 \end{array} \right] = \left[ \begin{array}{c} r + 2s + 3t \\ s + t \\ r + t \end{array} \right] \end{equation*}$

leading to equations , , and for real numbers , , and . But this time there is no solution as the reader can verify, so $\vect{w}$ is not a linear combination of $\vect{x}$ , $\vect{y}$ , and $\vect{z}$ .

Our interest in linear combinations comes from the fact that they provide one of the best ways to describe the general solution of a homogeneous system of linear equations. When
solving such a system with variables $x_1, x_2, \dots, x_n$ , write the variables as a column matrix: $\vect{x} = \left[ \begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right]$ . The trivial solution is denoted $\vect{0} = \left[ \begin{array}{c} 0 \\ 0 \\ \vdots \\ 0 \end{array} \right]$ . As an illustration, the general solution in
Example 1.3.1 is , , , and , where is a parameter, and we would now express this by
saying that the general solution is $\vect{x} = \left[ \begin{array}{r} -t \\ t \\ t \\ 0 \end{array} \right]$ , where is arbitrary.

Now let $\vect{x}$ and $\vect{y}$ be two solutions to a homogeneous system with variables. Then any linear combination $s\vect{x} + t\vect{y}$ of these solutions turns out to be again a solution to the system. More generally:

$\begin{equation*} \mbox{ Any linear combination of solutions to a homogeneous system is again a solution.} \end{equation*}$

In fact, suppose that a typical equation in the system is $a_1x_1 + a_2x_2 + \dots + a_nx_n = 0$ , and suppose that

$\vect{x} = \left[ \begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right]$ , $\vect{y} = \left[ \begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_n \end{array} \right]$ are solutions. Then $a_1x_1 + a_2x_2 + \dots + a_nx_n = 0$ and
$a_1y_1 + a_2y_2 + \dots + a_ny_n = 0$ .
Hence $s\vect{x} + t\vect{y} = \left[ \begin{array}{c} sx_1 + ty_1 \\ sx_2 + ty_2 \\ \vdots \\ sx_n + ty_n \end{array} \right]$ is also a solution because

$\begin{align*} a_1(sx_1 + ty_1) &+ a_2(sx_2 + ty_2) + \dots + a_n(sx_n + ty_n) \\ &= [a_1(sx_1) + a_2(sx_2) + \dots + a_n(sx_n)] + [a_1(ty_1) + a_2(ty_2) + \dots + a_n(ty_n)] \\ &= s(a_1x_1 + a_2x_2 + \dots + a_nx_n) + t(a_1y_1 + a_2y_2 + \dots + a_ny_n) \\ &= s(0) + t(0)\\ &= 0 \end{align*}$

A similar argument shows that Statement 1.1 is true for linear combinations of more than two solutions.

The remarkable thing is that every solution to a homogeneous system is a linear combination of certain particular solutions and, in fact, these solutions are easily computed using the gaussian algorithm. Here is an example.

Solve the homogeneous system with coefficient matrix

$\begin{equation*} A = \left[ \begin{array}{rrrr} 1 & -2 & 3 & -2 \\ -3 & 6 & 1 & 0 \\ -2 & 4 & 4 & -2 \\ \end{array} \right] \end{equation*}$

Solution:

The reduction of the augmented matrix to reduced form is

$\begin{equation*} \left[ \begin{array}{rrrr|r} 1 & -2 & 3 & -2 & 0 \\ -3 & 6 & 1 & 0 & 0 \\ -2 & 4 & 4 & -2 & 0 \\ \end{array} \right] \rightarrow \def\arraystretch{1.5} \left[ \begin{array}{rrrr|r} 1 & -2 & 0 & -\frac{1}{5} & 0 \\ 0 & 0 & 1 & -\frac{3}{5} & 0 \\ 0 & 0 & 0 & 0 & 0 \\ \end{array} \right] \end{equation*}$

so the solutions are $x_1 = 2s + \frac{1}{5}t$ , , $x_3 = \frac{3}{5}$ , and by gaussian elimination. Hence we can write the general solution $\vect{x}$ in the matrix form

$\begin{equation*} \vect{x} = \left[ \begin{array}{r} x_1 \\ x_2 \\ x_3 \\ x_4 \end{array} \right] = \left[ \begin{array}{c} 2s + \frac{1}{5}t \\ s \\ \frac{3}{5}t \\ t \end{array} \right] = s \left[ \begin{array}{r} 2 \\ 1 \\ 0 \\ 0 \end{array} \right] + t \left[ \begin{array}{r} \frac{1}{5} \\ 0 \\ \frac{3}{5} \\ 1 \end{array} \right] = s\vect{x}_1 + t\vect{x}_2. \end{equation*}$

Here $\vect{x}_1 = \left[ \begin{array}{r} 2 \\ 1 \\ 0 \\ 0 \end{array} \right]$ and $\vect{x}_2 = \left[ \begin{array}{r} \frac{1}{5} \\ 0 \\ \frac{3}{5} \\ 1 \end{array} \right]$ are particular solutions determined by the gaussian algorithm.

The solutions $\vect{x}_1$ and $\vect{x}_2$ in Example 1.3.5 are denoted as follows:

The gaussian algorithm systematically produces solutions to any homogeneous linear system, called basic solutions, one for every parameter.

Moreover, the algorithm gives a routine way to express every solution as a linear combination of basic solutions as in Example 1.3.5, where the general solution $\vect{x}$ becomes

$\begin{equation*} \vect{x} = s \left[ \begin{array}{r} 2 \\ 1 \\ 0 \\ 0 \end{array} \right] + t \left[ \begin{array}{r} \frac{1}{5} \\ 0 \\ \frac{3}{5} \\ 1 \end{array} \right] = s \left[ \begin{array}{r} 2 \\ 1 \\ 0 \\ 0 \end{array} \right] + \frac{1}{5}t \left[ \begin{array}{r} 1 \\ 0 \\ 3 \\ 5 \end{array} \right] \end{equation*}$

Hence by introducing a new parameter we can multiply the original basic solution $\vect{x}_2$ by 5 and so eliminate fractions.

For this reason:

Any nonzero scalar multiple of a basic solution will still be called a basic solution.

In the same way, the gaussian algorithm produces basic solutions to every homogeneous system, one for each parameter (there are no basic solutions if the system has only the trivial solution). Moreover every solution is given by the algorithm as a linear combination of
these basic solutions (as in Example 1.3.5). If has rank , Theorem 1.2.2 shows that there are exactly parameters, and so basic solutions. This proves:

Find basic solutions of the homogeneous system with coefficient matrix , and express every solution as a linear combination of the basic solutions, where

$\begin{equation*} A = \left[ \begin{array}{rrrrr} 1 & -3 & 0 & 2 & 2 \\ -2 & 6 & 1 & 2 & -5 \\ 3 & -9 & -1 & 0 & 7 \\ -3 & 9 & 2 & 6 & -8 \end{array} \right] \end{equation*}$

Solution:

The reduction of the augmented matrix to reduced row-echelon form is

$\begin{equation*} \left[ \begin{array}{rrrrr|r} 1 & -3 & 0 & 2 & 2 & 0 \\ -2 & 6 & 1 & 2 & -5 & 0 \\ 3 & -9 & -1 & 0 & 7 & 0 \\ -3 & 9 & 2 & 6 & -8 & 0 \end{array} \right] \rightarrow \left[ \begin{array}{rrrrr|r} 1 & -3 & 0 & 2 & 2 & 0 \\ 0 & 0 & 1 & 6 & -1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} \right] \end{equation*}$

so the general solution is , , , , and where , , and are parameters. In matrix form this is

$\begin{equation*} \vect{x} = \left[ \begin{array}{r} x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \end{array} \right] = \left[ \begin{array}{c} 3r - 2s - 2t \\ r \\ -6s + t \\ s \\ t \end{array} \right] = r \left[ \begin{array}{r} 3 \\ 1 \\ 0 \\ 0 \\ 0 \end{array} \right] + s \left[ \begin{array}{r} -2 \\ 0 \\ -6 \\ 1 \\ 0 \end{array} \right] + t \left[ \begin{array}{r} -2 \\ 0 \\ 1 \\ 0 \\ 1 \end{array} \right] \end{equation*}$

Hence basic solutions are

$\begin{equation*} \vect{x}_1 = \left[ \begin{array}{r} 3 \\ 1 \\ 0 \\ 0 \\ 0 \end{array} \right], \ \vect{x}_2 = \left[ \begin{array}{r} -2 \\ 0 \\ -6 \\ 1 \\ 0 \end{array} \right],\ \vect{x}_3 = \left[ \begin{array}{r} -2 \\ 0 \\ 1 \\ 0 \\ 1 \end{array} \right] \end{equation*}$

Find All Solutions to System of Linear Equations

Source: https://ecampusontario.pressbooks.pub/linearalgebrautm/chapter/chapter-1-system-of-linear-equations/

Livingstone-Learmonth Happled

Find All Solutions to System of Linear Equations

1 System of Linear Equations

Elementary Operations

Rank

Linear Combinations and Basic Solutions

Menu Halaman Statis